中心差分法求相对位移时程曲线
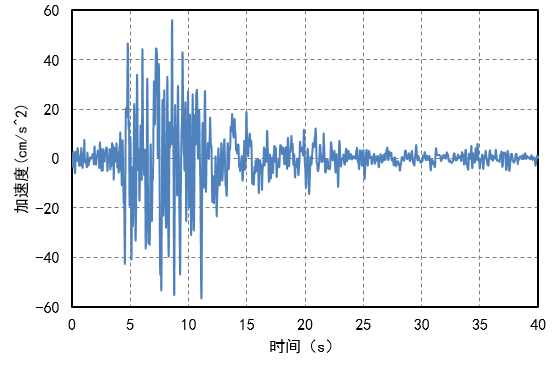
中心差分法求相对位移时程曲线
Charm_Hu源码依附在文章最后,读者可跳过讲解部分可直接下载。
中心差分法原理
从上述资料中可以看出,以线弹性体系为例,有:
只要我们知道了第i时刻、i-1时刻结构体系的位移(严格来说叫相对位移,下同)和第i时刻地震动加速度$\ddot { X } _ { g , i }$,就可以求出第i+1时刻结构的位移。上述资料假设了第0时刻的位移、速度为0,现不妨更为普遍的设其为$X_{0}$和$\dot{X}_{0}$,则有:
联立即得:
式中${\ddot X}_0$可根据第0时刻的多自由度结构体系运动微分方程求得:
由此,启动条件便确定了,再根据(1)式递推即可。
多自由度结构体系的中心差分法的MATLAB源码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31function [x, v, a] = MDOF_CentralDifference(m, k, c, P, x0, v0, dt, n)
x = zeros(size(m,1), n); % 位移
v = zeros(size(m,1), n); % 速度
a = zeros(size(m,1), n); % 加速度
x(:, 1) = x0; % 设置初始位移
v(:, 1) = v0; % 设置初始速度
a(:, 1) = m\(P(:, 1) - c * v(:, 1) - k * x(:, 1)); % 计算初始加速度
x_1 = x(:, 1) - dt .* v(:, 1) + dt^2 / 2 .* a(:, 1); % 计算 X_(-1)
P_eq = zeros(size(m)); % 初始化等效力
k_eq = m ./ dt^2 + c ./ (2 * dt); % 有效弹簧系数
b1 = m ./ dt^2 - c ./ (2 * dt); % 一阶阻尼项系数
b2 = k - 2 .* (m ./ dt^2); % 二阶质量项系数
P_eq(:, 1) = P(:, 1) - b1 * x_1 - b2 * x(:, 1); % 计算第一步的等效力
x(:, 2) = k_eq\P_eq(:, 1) ; % 计算第二步的位移
for i = 2:n-1
P_eq(:, i) = P(:, i) - b1 * x(:, i-1) - b2 * x(:, i); % 计算等效力
x(:, i+1) = k_eq\P_eq(:, i); % 计算位移
v(:, i) = (x(:, i+1) - x(:, i-1)) ./ (2 * dt); % 计算速度
a(:, i) = (x(:, i+1) - 2 * x(:, i) + x(:, i-1)) ./ dt^2; % 计算加速度
end
P_eq(:, n) = P(:, n) - b1 * x(:, n-1) - b2 * x(:, n);
xx = k_eq\P_eq(:, n);
v(:, n) = (xx - x(:, n-1)) ./ (2 * dt); % 计算最后一步的速度
a(:, n) = (xx - 2 * x(:, n) + x(:, n-1)) ./ dt^2; % 计算最后一步的加速度
end
示例
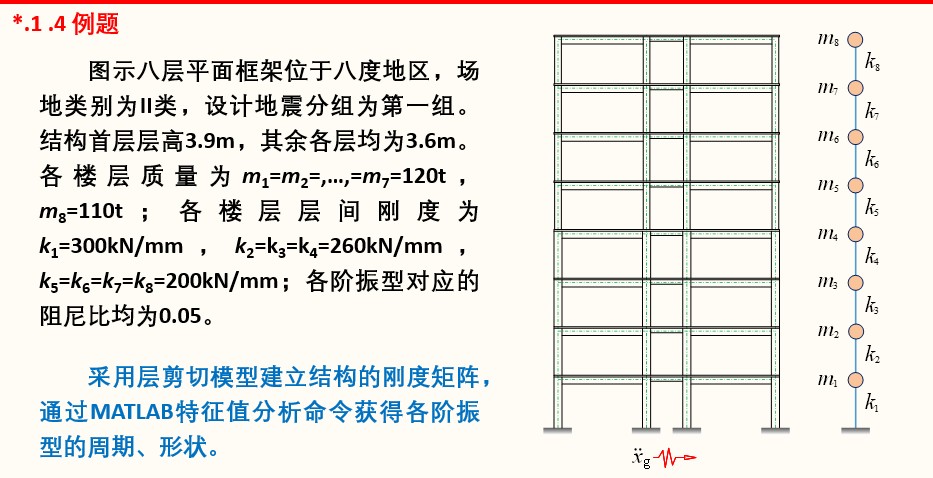
已知各阶振型及周期如下图所示,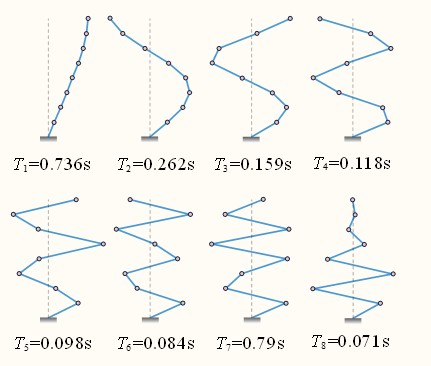
试利用中心差分法求其在ELCentro波作用下的位移时程曲线。
结构基本信息
采用国际单位制:t\N\mm\s;
质量矩阵
易知结构质量矩阵为对角矩阵,有:1
M = diag([120, 120, 120, 120, 120, 120, 120, 110]);
刚度矩阵
采用层剪切模型,易知n个自由度糖葫芦串模型的刚度矩阵表达式如下所示:
故生成刚度矩阵如下:1
2
3
4
5
6
7
8k = [300, 260, 260, 260, 200, 200, 200, 200]*1000 ; %各层层间刚度
K = zeros(8,8);
for i = 1:7 %层剪切模型的刚度矩阵
K(i,i) = k(i) + k(i+1);
K(i+1,i) = -k(i+1);
K(i,i+1) = -k(i+1);
end
K(8,8) = k(8);
阻尼矩阵
采用瑞利阻尼,即$C=\alpha_0M+\alpha_1K$,其中两个系数$\alpha_0$和$\alpha_1$由下式确定:
其中,$\omega _ { i }$,$\xi _ { i }$表示第i振型的频率和阻尼比。
本题采用第1、2振型的频率和阻尼比,求解得到$\alpha_0 = 0.6296$和$\alpha_1 = 0.003075$.1
2C = 0.6296*M + 0.003075*K;
xi = 0.05; %各阶振型的阻尼比
读取地震动加速度时程信息
值得注意的是,ElCentro.txt文件中,加速度单位为g,也就是$9.8m/s^2$,注意转化。1
2
3
4
5
6
7
8
9
10a=textread('ElCentro.txt'); % 先将地震动加速度记录存放在a中,用于下面的处理
[i,j]=size(a); % 地震数组维数
RecordLength=i*j; % 记录步数
A=zeros(RecordLength,2); % 定义处理后的地震动加速度时程数组,有两列,第一列存放时间,第二列存放对应地震动加速度值
A(1:RecordLength,1)= 0:0.01:(RecordLength-1)*0.01; % 在A中输出时间变量,式中的0.01为记录间隔
for n1 = 1:1:i % 用双重for循环将a中的记录按顺序放入A中
for n2=1:1:j
A((n1-1)*j+n2,2)=a(n1,n2)*9.8*1000; % g(9.8 m/s2) 转化为 mm/s2
end
end
定义地震动等效动荷载矩阵
即:$P=-M\left\{1\right\}{\ddot x}_g$.1
2
3
4
5onevector = ones(size(M,2),1);
P = zeros(size(M,1),RecordLength);
for i = 1:RecordLength
P(:,i) = -(M*onevector).*A(i,2);
end
调用中心差分法函数进行求解
1 | x0=zeros(8,1); % 相对运动的初位移(数值积分用) |
绘制第1层的位移时程曲线
1 | figure |
上方layer_num是层号,可随意调整,输出该层位移的时程曲线。
文件下载
点击下载:ElCentro.txt、MDOF_CentralDifference.m、MDOF_RelativeDisp.m.
将上述三个文件放在同一个文件夹下即可在MATLAB上运行,没安装MATLAB的同学可以试试MATLAB online.