力学基础和专业基础(持续更新)

Charm_Hu2023-10-052024-03-17

材料力学

最近学了拉压、扭的部分，大致思路都是强度-刚度-应变能，公式也很类似。下面分享几个比较有意思的点：
第一个是小变形放大图，常用来解决超静定问题，依靠平衡方程和变形协调方程，再加上本构方程。这里的变形协调其实就是后面力法方程的本质，可以说是埋下伏笔了。
第二个是功互等定理和位移互等定理，在材料力学中只是当作附加部分讲了讲，并没有涉及其本质，具体推导可以参见 《结构力学》（龙驭球）第五章最后一节，用虚功原理予以解释，此外，那里还介绍了两个互等定理。注意：上述四个互等定理只适用于线性变形体系。
剪应力互等定理新的理解
详细可以参考一下这篇文章。感觉与以前理解不同的地方在于：取出来的单元体实际上六个面均有力，每个面有两个方向的切应力和一个正应力，相对的面上应力相等。（他给出的解释是单元体足够小，可以看作一个点，故相对的两个面力相等）
1
https://www.zhihu.com/question/21070058
非对称纯弯曲梁的正应力（《材料力学》下册1-1节）
推导得到了广义弯曲正应力，有一个印象即可。对于非对称弯曲，应该是指梁不具有对称平面，或者梁具有对称平面，但外力不作用在该平面内，梁将发生非对称弯曲。
开口薄壁截面梁的剪应力流和弯曲中心
截面剪应力流的方向确定：(简单的根据：与剪力平行的截面上剪应力流与剪力平行，例如矩形截面，工字形截面的腹板等。)
1. 根据截面弯矩和中性轴确定拉压应力；(方便下一步由正应力合成轴力)
2. 切开构件，取隔离体，根据隔离体轴力平衡，非自由面取切应力(一般只有3个非自由面，其中有两个是前后轴力方向，另一个面取剪应力来平衡)，然后再根据剪应力互等定理确定前后两个非自由面上剪应力方向。
而弯曲中心的确定方法见《材料力学合并文档》P252.核心就是截面上剪应力合成到某点，只有力而无力偶，该点即为弯曲中心。
重点是弯曲中心（剪切中心）的作用：非对称截面梁发生平面弯曲的条件：外力必须作用在通过弯曲中心且平行于形心主惯性平面（或与之重合）的平面内。

结构力学

单自由度结构自由振动自振频率的求解

今天复习了结构动力学基础中一个重要问题——单自由度结构体系自由振动自振频率的求解。困扰了将近一年的问题今天终于搞定了。顺便复习了科氏加速度等几个概念，具体参见《理论力学》P190.

虚功原理、虚力原理与虚位移原理辨析

根据上述资料，可知虚功原理表述为：
如果力系满足平衡方程，变形状态满足协调方程，则虚功方程（下式）成立。

$\begin{equation*} \sum F _ { P } \Delta + \sum F _ { R K } C _ { K } = \sum \int _ { A } ^ { B } ( Mk+ F _ { N } \varepsilon + F _ { Q } \gamma _ { 0 } ) d s \end{equation*}$

然后，单独一个虚功方程只是必要条件，而不是充分条件。
由此引出一个想法：能否将虚功原理及其虚功方程(上式)加以改造，使改造后的“虚功型方程”（指：用虚功形式表示的方程）成为变形协调方程或力系平衡方程的充分必要条件呢？于是，就产生了下列两个“虚功型原理”一虚力原理和虚位移原理。

虚力原理：
在虚设力系满足平衡方程且具有任意性的前提下，如果虚力方程（下图）成立，则待检查的变形状态必满足变形协调方程。反之，在上述前提下，如果已知该变形状态满足变形协调方程，则虚力方程必成立。综合起来，在上述前提下，虚力方程是变形协调方程的充分必要条件。

虚位移原理：
在虚设变形状态满足变形协调方程并具有任意性的前提下，如果虚位移方程(下式)成立，则待检查的力系必满足平衡方程。反之，在上述前提下，如果已知该力系满足平衡方程，则虚位移方程必成立。综合起来，在上述前提下，虚位移方程是力系平衡方程的充分必要条件。

结构对称性探究

正是由于上述结论，可将奇/偶跨对称结构简化，简化的要求是与原结构等效，表现为力和变形条件。
值得注意的是，对称轴处的荷载要减半，当然最终结果加和时，对称轴处相当于加了两次，合理的。 可参考下面这两篇文章：

1 2	文章一：https://zhuanlan.zhihu.com/p/576399081 文章二：https://zhuanlan.zhihu.com/p/147244195

对称边界与反对称边界位移条件

最近学习了水哥ansys初级教程，其中谈到对称边界和反对称边界位移条件时时，有：

受对称载荷作用则对称面上的位移条件为
1. 垂直于对称面的移动位移分量为零。
2. 绕平行于对称面的两相互垂直的轴的转动位移分量均为零。
受反对称载荷作用则对称面上的位移条件为
1. 平行于对称面的移动位移分量为零；
2. 绕方向矢量垂直于对称面的轴的转动位移分量为零。

结构平衡-几何矩阵互伴定理

定理证明：

龙驭球《结构力学》下册第14章

定理的运用，以老师留的习题为例：

上述资料是按照矩阵分析一步步来的，略显繁琐，谭启阳老师讲了另一种方法，如下面这个所示，关键就是力系平衡和变形协调！

其实，通过结构平衡-几何矩阵互伴定理可以推出结构刚度矩阵正定的，这里我以上述题目为例，验证如下：
已知：

$Af = F$ $BX = \Delta$

且

$A = {B^T}$

证明：
现设矩阵C如下：
$$C = \left[ {\begin{array}{*{20}{c}}{\frac{{EA}}{{{l_1}}}}&0&0\\0&{\frac{{EA}}{{{l_2}}}}&0\\0&0&{\frac{{EA}}{{{l_3}}}}\end{array}} \right]$$

将方程$BX = \Delta$左右两端同左乘C，则有：

$CBX = C\Delta$

又根据$C\Delta = f$，则有：

$BCX = f$

方程两边再同左乘$A$，则有：

$ACBX = Af = F$

由于$A = {B^T}$，推出：

${B^T}CBX = F$

显然，刚度矩阵$K = {B^T}CB$，现令$C = {D^T}D$，$Q = DB$，则刚度矩阵转化为：

$K = {Q^T}Q$

由于$Q$是可逆矩阵，根据线性代数知识知，$K$必为正定矩阵。
得证！

结构刚度矩阵推导的两种方法

分层法迭代过程

土力学

由于较少从事这方面研究，目前待更新！！！

混凝土结构基本原理

钢筋混凝土受扭构件承载力公式推导的两种方法

此文章写于大三下学期，目前来看，这两种方法的本质相同，第一种根据q相同求得，第二种根据Tu相同求得，但又有

$\begin{equation*} T_{u} = 2qA_{cor} \end{equation*}$

故其本质相同。

钢结构基本原理

稳定性

轴心受压、受弯及压弯构件的宽厚比限值

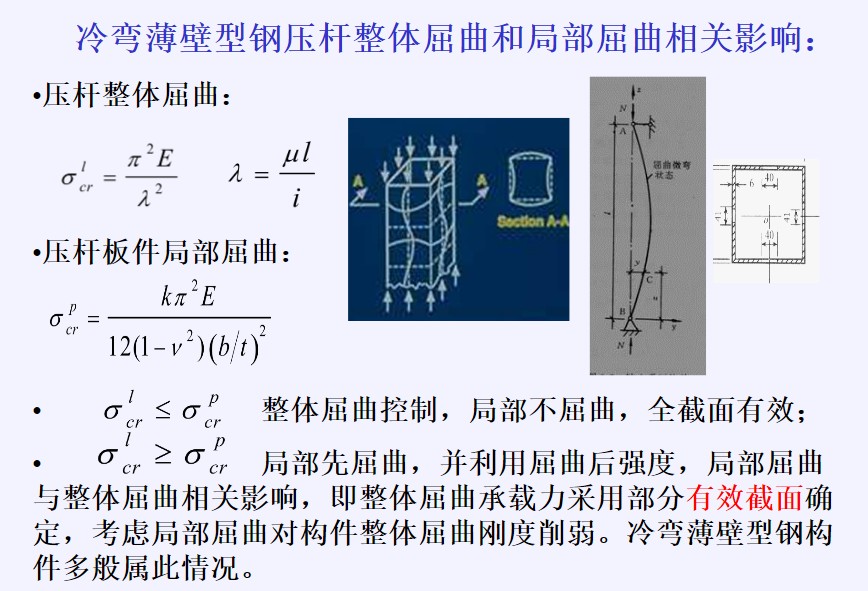
宽厚比限值的根本目的是为了防止局部失稳先于整体失稳。由此，规范采用等稳定性原则，即板件屈曲应力不小于构件屈曲应力。

$\begin{equation*} \sigma_{crx}\geq \sigma _{cr} \end{equation*}$

同时，根据以何种状态下（例如弹性）抗力抵抗该种状态下效应即为该种状态设计，故当板件弹性屈曲应力不小于构件弹性屈曲应力，为弹性设计。

$\begin{equation*} \frac{b_{1}}{t}\leq 15 \varepsilon _{k} \end{equation*}$

这些天(2023-10-17)恰好在学习冷弯薄壁型钢的设计，这里举例如下：

土木工程施工

土方工程

基坑支护

基坑支护包括一般基坑支护和深基坑支护。
深基坑支护方法有：

水泥土挡墙式支护结构：采用深层搅拌机就地将土和输入的水泥浆强行搅拌，形成连续搭接的水泥土柱状加固体挡墙。
排桩与板墙式支护结构：开挖前在基坑周围设置砼灌注桩或钢板桩，桩的排列有间隔式、双排式和连续式，桩顶设置砼连系梁或锚桩、拉杆。
土钉墙支护：在天然土体通过钻孔、插筋、注浆来设置土钉(亦称砂浆锚杆)并与喷射砼面板相结合，形成类似重力挡墙的土钉墙，以抵抗墙后的土压力，保持开挖面的稳定。
土层锚杆支护结构：在深基础立壁上钻孔，并达到一定深度，然后在孔内放入钢筋等材料，灌入泥浆或化学浆液，使其与土层结合成为抗拉（拔）力强的锚杆，将立壁土体侧压力传至稳定土层。

在实际工程中，其实上述某些方法可组合使用，例如挡土灌注桩（排桩）+土层锚杆等。