振型分解反应谱法及相关系数推导
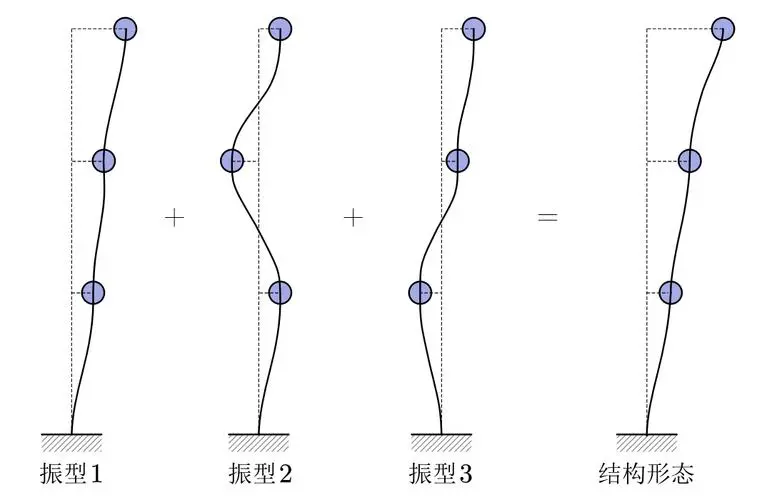
振型分解反应谱法及相关系数推导
Charm_Hu整理自结构设计杂谈. 理解本文需要阅读一下上述链接中资料或本身具有一定基础!
振型分解反应谱只适用于弹性分析。
下面开始正式推导!
振型分解法
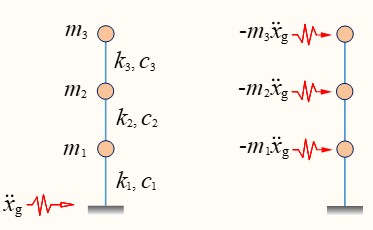
易知多自由度(这里设为n)结构体系在地震动作用下运动微分方程为:
易知该结构体系无阻尼自由振动微分方程为$M\ddot X + KX = 0$,由高等数学知识可知,其解为$X = \varphi \sin \left( {wt} \right)$,再代入无阻尼自由振动微分方程中,由于$\omega \ne 0$,$\varphi \ne {0}$,即得:
也即:
由线性代数知识知,这等效于求${M^{ - 1}}K$的特征值和特征向量。于是解特征方程:
由于结构刚度矩阵K是正定的,一定能得到n个正特征值(允许有重根)和n个线性无关的特征向量!
为啥能得到?见开头所讲资料;
而且对于任意两个不同频率($\omega_{i}$、$\omega_{j}$)所对应的振型向量($\varphi_{i}$、$\varphi_{j}$)关于质量矩阵M、阻尼矩阵C和刚度矩阵K是正交的!
事实上,对于重根的情况,也可以找到两个振型关于上述矩阵正交。具体原理可参加《结构动力学》(Chopra 著)。
下面以质量矩阵M为例:
将$\varphi _i$和$\varphi _j$代入式(1)中,得:
将式(4)等式两边同乘以$\varphi _j^T$,式(5)等式两边同乘$\varphi _i^T$,并等式两边同时转置,有:
M、K由于是对称矩阵,其转置等于自身。
式(6)-式(7),得到:
由于$\omega_{i} \ne \omega_{j}$,则有
得证!
由于n个特征向量线性无关,故可作为一组基来表示结构的位移,即$X = \sum {({q_i(t)}{\varphi _i})} $,t表示第t时刻,将X表达式代入式(1),有:
$$ M\{ \sum {\left( {{{\ddot q}_i}{\varphi _i}} \right)} \} + C\{ \sum {\left( {{{\dot q}_i}{\varphi _i}} \right)} \} + K\{ \sum {\left( {{q_i}{\varphi _i}} \right)} \} = - M\{ 1\} {\ddot x_g} $$
上式等式两边同左乘$\varphi _i^T$,根据振型向量的正交性,有:
也即:
记${M_i} = \varphi _i^TM{\varphi _i},{C_i} = \varphi _i^TC{\varphi _i},{K_i} = \varphi _i^TK{\varphi _i}{q_i}$,分别称为第i阶振型的广义质量、阻尼和刚度矩阵。
于是就有:
式(9)还可以表示为:
$$ {M_i}{\ddot q_i} + {C_i}{\dot q_i} + {K_i}{q_i} = - \frac{{\varphi _i^TM\{ 1\} }}{M_i}{M_i}{\ddot x_g}$$
现记${\gamma _i} = \frac{ {\varphi _i^TM\{ 1\} } }{ { {M_i} } } = \frac{ {\varphi _i^TM\{ 1\} } }{ {\varphi _i^TM{\varphi _i} } }$,称为第i阶振型的振型参与系数。
易知振型参与系数满足如下关系:
证明如下:
式(10)等式两端同左乘${\varphi _i}^TM$,根据振型的正交性,有:
由此,显然有:
得证!
令 ${D_i} = \frac{q_i}{\gamma _i}$,记为第i阶振型的地震响应时程。
于是式(9)就转化为:
从上式可以看出,第i振型的振动满足单自由度结构体系受迫振动运动微分方程。
对于给定的地震动时程,可以利用求解单自由度体系方法获得第i振型的地震响应时程$D_i$。由于i的任意性,可以看出在t时刻,多自由度结构体系各振型均满足单自由度结构体系受迫振动运动微分方程。通过振型叠加,即可获得各自由度的位移相对时程:
这种利用振型的正交性,将多自由度结构体系振动解耦成单自由度结构体系振动的方法称为振型分解法!
振型分解反应谱法
在前述基础上,引入反应谱的概念。
常用的反应谱包括加速度反应谱和位移反应谱(亦称伪加速度反应谱),下面以位移谱为例进行推导。
位移谱定义:
$$\alpha = \frac{{{K_i}{D_{i\_\max }}\left( T \right)}}{{{M_i}g}}$$
对于第i阶振型,其地震响应时程最大值的标准值为:
$${D_{i\_k}} = \frac{{{\alpha _i}{M_i}g}}{{{K_i}}} = \frac{{{\alpha _i}g}}{{\omega _i^2}}$$
则第i振型最大位移为:
因为${\gamma _i}{\varphi _i}$是定值,$D_{i}$取最大,即$X_i$取最大。
我们认为结构处于最大位移时最不利,相应的地震作用为:
$$
\begin{align*}
F_i &= KX_i = KD_{i\_k}\gamma_i\varphi_i = K\frac{\alpha_ig}{\omega_i^2}\gamma_i\varphi_i = \frac{\alpha_ig}{\omega_i^2}\gamma_iMM^{-1}K\varphi_i \\
&= \frac{\alpha_ig}{\omega_i^2}\gamma_iM\omega_i^2\varphi_i \\
&= \tag{11}\alpha_i\gamma_igM\varphi_i
\end{align*}
$$
这样,我们就得到了第i阶振型所对应的地震作用啦!
对于第j个质点,其所受地震作用为:
作用效应组合:采用平方和开平方法(SRSS法)
振型参与质量系数与振型有效质量系数
疑惑起源:
《抗规》中提到,振型个数一般需要取振型参与质量累计达到总质量90%所需的振型数。
第i阶振型的地震作用:
上式可以写成:
$${F_i} = {\alpha _i}{\gamma _i}Mg{\varphi _i} = \frac{{{\alpha _i}g}}{{\ddot x}_{g\_\max }}M{\ddot x_{g\_\max }}{\gamma _i}{\varphi _i}$$
这里我们称 $\frac{ { {\alpha _i}g} }{ { { {\ddot x}_{g_\max } } } }$ 为动力放大系数,记为$\beta$,即:
其中$M{\ddot x_{g_\max }}{\gamma _i}{\varphi _i}$为地震动最大加速度的等效动荷载在第i阶振型上的分量。
则$F_i$产生的效应可以写成:
$${S_i} = S\left( {{F_i}} \right) = \beta S\left( {M{{\ddot x}_{g\_\max }}{\gamma _i}{\varphi _i}} \right)$$
可见,地震动最大加速度的等效动荷载在第i阶振型上的分量引起的结构响应越大,地震响应系数$\alpha_{i}$越大,则第i振型对应的效应就越大.
对于线弹性体系,有:
$$S\left( {M\{ 1\} {{\ddot x}_{g\_\max }}} \right) = S\left( {M\sum {\left( {{\gamma _i}{\varphi _i}} \right){{\ddot x}_{g\_\max }}} } \right) = \sum {\left( {S\left( {M{{\ddot x}_{g\_\max }}{\gamma _i}{\varphi _i}} \right)} \right)}$$
令
$${\mu _{S\_j}} = \frac{{\sum\limits_{i = 1}^j {\left( {S\left( {M{{\ddot x}_{g\_\max }}{\gamma _i}{\varphi _i}} \right)} \right)} }}{{\sum\limits_{i = 1}^n {\left( {S\left( {M{{\ddot x}_{g\_\max }}{\gamma _i}{\varphi _i}} \right)} \right)} }}$$
称$\mu_{S_j}$为效应S的振型有效质量系数。
一般来讲,结构的基底剪力(首层剪力)能够很好地反映结构的整体响应。
式(12)为第i阶振型第j个质点所受地震水平力,则基底剪力可以表示为:
易知基底剪力可以表示为:
则基底剪力的振型有效质量系数$\mu _{BS_j}$为:
$$
\begin{align*}
{\mu _{BS\_j}} &= \frac{{\sum\limits_{i = 1}^j {\left( {{{\{ 1\} }^T}{\alpha _i}{\gamma _i}Mg{\varphi _i}} \right)} }}{{\sum\limits_{i = 1}^n {\left( {{{\{ 1\} }^T}{\alpha _i}{\gamma _i}Mg{\varphi _i}} \right)} }} = \frac{{\sum\limits_{i = 1}^j {\left( {{{\{ 1\} }^T}{\gamma _i}M{\varphi _i}} \right)} }}{{{{\{ 1\} }^T}M\sum\limits_{i = 1}^n {\left( {{\gamma _i}{\varphi _i}} \right)} }} = \frac{{\sum\limits_{i = 1}^j {\left( {{{\{ \sum {{\gamma _i}{\varphi _i}} \} }^T}{\gamma _i}M{\varphi _i}} \right)} }}{{{{\{ 1\} }^T}M\{ 1\} }} \\
&= \frac{{\sum\limits_{i = 1}^j {\left( {{\gamma _i}\varphi _i^T{\gamma _i}M{\varphi _i}} \right)} }}{{\sum\limits_{i = 1}^n {{m_i}} }}\\
&= \frac{{\sum\limits_{i = 1}^j {\left( {\gamma _i^2{M_i}} \right)} }}{{\sum\limits_{i = 1}^n {{m_i}} }}
\end{align*}
$$
进一步,令
称$M_i^*$为第i阶振型的基底剪力振型参与质量。
自然而言,有第i阶振型的基底剪力振型参与质量系数:
易知其满足:
如前述所说,结构的基底剪力能够很好地反映结构的整体响应,所以我们一般就采用基底剪力振型参与质量系数和基底剪力有效质量系数,并简称振型参与质量系数与振型有效质量系数!
先写到这吧,还挺多的呢,敬请期待(☆▽☆)