Kriging 模型
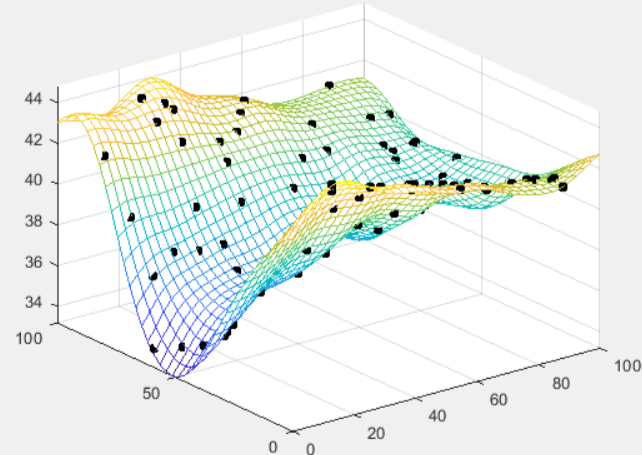
Kriging 模型
Charm_Hu最近写毕业论文用到Kriging模型,经过一周的摸索,对其有一定的了解,遂作此笔记。
接下来我将从一个萌新的角度逐步带你揭开kriging模型神秘的面纱!
初识kriging 模型
一开始接触到这个名词,大家较多的会看看B站上有没有相关教程,由此映入眼帘的就是猪星人这位up主的视频1,从那里大家就会发现kriging有现成的matlab工具箱2,如下所示:
而且工具箱也提供了几个例子,简单好上手,如CSDN上那篇博客介绍。(见下图)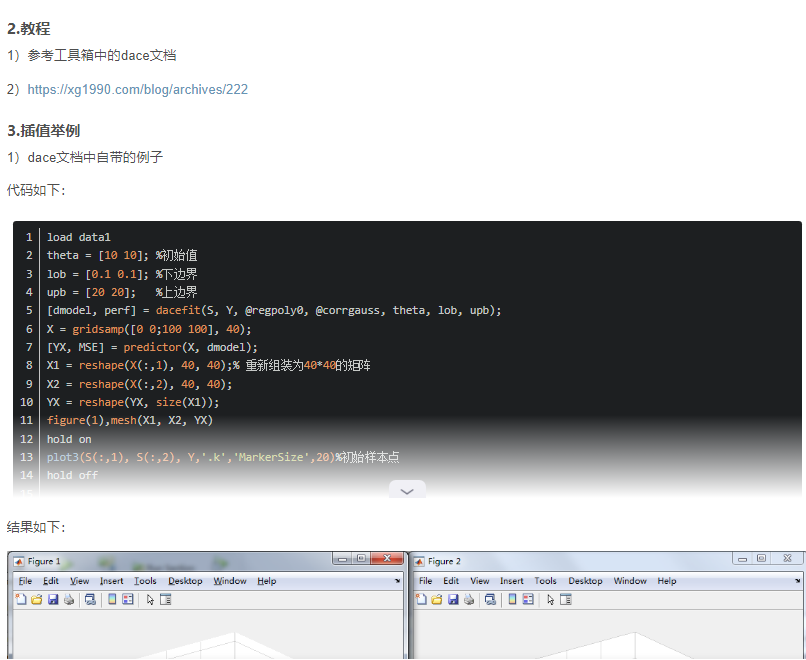
于是大家兴奋不已,如获珍宝,难道到这就结束了?噩梦才刚开始!
紧接着,大家就会像,Kriging模型理论是啥,毕竟大家论文前面总要凑字数的嘛😁😁😁
于是你就会看到上述CSDN上博客写着的教程:
1)参考工具箱中的dace文档5
2)https://xg1990.com/blog/archives/222
显然,对于dace自带的说明书,全英文,我们直呼不能接受!而选项2),xg老师那篇文章3,点进去一看,中文,哎,兴趣就来了。
这里我推荐你一定要把xg1990大佬的这篇文章认真研读一遍,这篇文章算是我接触过的最易理解的关于kriging模型的介绍了!
pdf不显示的话刷新一下就好了!
文中推导需要用到的一些概率统计的基本公式,这里总结一下:
$$Cov\left( {X,Y} \right) = E\left[ {\left( {X - E\left( X \right)} \right)\left( {Y - E\left( Y \right)} \right)} \right] = E\left( {XY} \right) - E\left( X \right)E\left( Y \right)$$ $$Var\left( X \right) = Cov\left( {X,X} \right) = E\left( {{X^2}} \right) - {E^2}\left( X \right)$$ $$Var\left( {X - Y} \right) = E\left[ {{{\left( {\left( {X - Y} \right) - E\left( {X - Y} \right)} \right)}^2}} \right] = Var\left( X \right) + Var\left( Y \right) - 2Cov\left( {X,Y} \right)$$ $${\left( {\sum\limits_{i = 1}^n {{x_i}} } \right)^2} = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {\left( {{x_i}{x_j}} \right)} } $$ $$Var\left( {\sum\limits_{i = 1}^n {{X_i}} } \right) = E\left[ {{{\left( {\sum\limits_{i = 1}^n {\left( {{X_i} - {\mu _i}} \right)} } \right)}^2}} \right] = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {E\left[ {\left( {{X_i} - {\mu _i}} \right)\left( {{X_j} - {\mu _j}} \right)} \right]} } = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {Cov\left( {{X_i},{X_j}} \right)} } $$看完上述xg1990大佬写的文章,整个人的心情瞬间舒畅,大佬文尾贴心地总结了Kriging模型建模步骤(如下图)。
于是我们就兴致冲冲开干,拿着dace工具箱想验算几篇论文。这里我们挑选两篇比较经典和较新的文章。
第一篇,韩忠华老师的文章4。
什么? y(x)可以被表述成下式:
$z(x)$竟然还是一个静态随机过程!
最后预测值竟然是:
我们的$\hat y\left( x \right) = \sum\limits_{i = 1}^n { {\omega _i}{y_i} }$这样通俗易懂的插值到哪里去了啊?
在xg1990大佬博客中那个半方差函数又去哪了呢?怎么又多出来个相关函数$R\left( {\theta ,{x_i},{x_j} } \right)$呢?
于是我们又点开一篇文章。
第二篇,查从燚老师(or学长)文章6。
kriging 模型又被表示成:
怎么回事,怎么又多了个f(x)啊?把人搞得晕头转向!
莫慌莫慌,接下来我会带你捋一遍!发车咯(●ˇ∀ˇ●)
Kriging 模型推导
Kriging模型一种插值模型,其插值结果定义为已知样本函数响应值的线性加权,即
其中$\omega _i$就是待求的权重系数,x是一个n维向量,n是输入参数个数。
为了计算这个加权系数,Kriging模型引入统计学假设:将未知函数看成是一个回归模型和一个随机过程构成,数学表达式如下:
$$\hat y\left( x \right) = {f^T}\left( x \right)\beta + z\left( x \right) = \sum\limits_{i = 1}^p {({f_i}\left( x \right)} \times {\beta _i}) + z\left( x \right)$$
其中,$f_i(x)$称为x的基函数(一般为多项式),${\beta}_i$称为x的回归模型系数,${f^T}\left( x \right)\beta$称为回归模型。
此处f(x)的具体表达式是啥呢?
见下图。
从上图我们就可以知道,$f_i(x)$有三种形式,分别对应于回归模型为常数(constant)、线性(linear)和二次项(quadratic)的情况。n为输入参数的个数。
噢噢,原来韩忠华老师那篇文章讲的是对应f(x)为常数的时候啊!同理,xg1990大佬那篇文章讲的也是f(x)为常数的情况!
z(x)是一个均值为0,方差为$\sigma^2$的随机过程,其协方差满足:
上式中$R\left( {\theta ,{x_i},{x_j} } \right)$称为相关函数,其只与空间距离有关(θ值一定时),距离为0时,其值为1,距离为无穷大时,其值为0,也就是说相关性随着距离增大而减小。
可能又有人要问了,这个相关函数是啥?
这里我们类比xg1990大佬提到的半方差函数,最后不是要得到$r = r\left( d \right)$嘛,也是与距离相关,故暂且认为相关函数充当了$r = r\left( d \right)$的作用!
对于这个相关函数的具体表达式,可见后面!
对于Kriging模型,权重系数$\omega _i$的取值直接影响到模型的精度,因此我们关注的重点是最优的权重系数$\omega _i$如何得到。要取得最优权重系数$\omega _i$,需要满足如下两个条件:
- 预测值满足无偏估计,$E\left( {\hat y\left( x \right)} \right) = y\left( x \right) = E\left( {y\left( x \right) } \right)$,即
. - 预测值的均方差(MSE)最小,即 $$\min E\left[ {{{\left( {\hat y\left( x \right) - y\left( x \right)} \right)}^2}} \right]$$
先定义一些后续推导需要用到的矩阵和向量。
基函数矩阵:
$$F = {\left[ {f^T\left( {{x_1}} \right),f^T\left( {{x_2}} \right),...,f^T\left( {{x_m}} \right)} \right]^T}$$
$$f\left( {{x_i}} \right) = \left[ {{f_1}\left( {{x_i}} \right),{f_2}\left( {{x_i}} \right),...,{f_p}\left( {{x_i}} \right)} \right]^T (i = 1,2,...,m)$$
这里m对应是m个样本点,p是一个样本点包含基函数的个数,$x_i$是一个向量。
以p=n+1为例,$f_1\left( x_i \right) = 1$, $f_2\left( x_i \right) = x_{i,1}$,…,$f_i^p\left( x \right) = x_{i,n}$.(i = 1,2,…,m)
回归模型系数向量:
随机过程向量:
权重系数向量:
响应值向量:
相关矩阵:
$$R=\begin{bmatrix}R(\theta,x_1,x_1)&...&R(\theta,x_1,x_m)\\...&&...\\R(\theta,x_m,x_1)&...&R(\theta,x_m,x_m)\end{bmatrix}$$
相关向量:
$${r_x} = \left[ {R\left( {\theta ,{x_1},x} \right),R\left( {\theta ,{x_2},x} \right),...,R\left( {\theta ,{x_m},x} \right)} \right]^T$$
根据条件(1),有
$$
\begin{align*}
E\left( {\hat y\left( x \right) - y\left( x \right)} \right) &= E\left[ {{\omega ^T}{y_s} - {f^T}\left( x \right)\beta - z} \right] = E\left[ {{\omega ^T}\left( {F\beta + Z} \right) - {f^T}\left( x \right)\beta - z} \right] \\
&= E\left[ {{\omega ^T}Z - z + {\omega ^T}F\beta - {f^T}\left( x \right)\beta } \right] \\
&= 0
\end{align*}
$$
由于$E\left( z \right) = 0$,故可得${\omega ^T}F - {f^T}\left( x \right) = 0$,等式两边同时转置,得
根据条件(2),有
$$
\begin{align*}
E\left[ {{{\left( {\hat y\left( x \right) - y\left( x \right)} \right)}^2}} \right]
&= E\left[ {{{\left( {{\omega ^T}Z - z} \right)}^2}} \right] \\
&= E\left[ {{{\left( {{z^2} + {\omega ^T}Z{Z^T}\omega } \right)}^2} - 2{\omega ^T}Zz} \right] \\
&= {\sigma ^2}\left( {1 + {\omega ^T}R\omega - 2{\omega ^T}r} \right)
\end{align*}
$$
要求:
要求Kriging模型的系数$\omega_i$,就必须同时满足式(1)和(2)。很容易就想到利用拉格朗日乘数法,构造如下拉格朗日函数:
$$L\left( {\omega ,\lambda } \right) = {\sigma ^2}\left( {1 + {\omega ^T}R\omega - 2{\omega ^T}r} \right) - \lambda \left( {{F^T}\omega - f\left( x \right)} \right)$$
对$\omega$和$\lambda$分别求偏导,得
解上述两式,得
再回代进$\hat y = {\omega ^T} {y_s}$,有
这里先给出$\beta$的最小二乘估计(证明后续给出):
最小二乘估计属于最大似然估计的一种形式8,最大似然估计是指在给定样本的情况下,得到某参数满足该样本出现概率最大的值,该值也称为该参数的最大似然估计值。
这样,式(3)就可以被表示为
通过式(4)就可以得到Kriging模型在未知点$x$的预测值了!
但是对于式(4)还有个问题,就是相关函数R中存在未知参数$\theta$,所以先要根据已知样本得到$\theta$的值,很显然需要通过最大似然估计来实现。
在介绍$\theta$的最大似然估计之前,先介绍相关函数R.
相关函数R
相关函数R可以表示成如下式子:
对于${ {R_k}\left( {\theta ,x_i^k,x_j^k} \right) }$,其具体表达式有如下几种:
$$ \begin{array}{|c|c|} \hline {函数名} & { {{R_k}\left( {\theta ,x_i^k,x_j^k} \right) } }\\ \hline {EXP} & { \exp \left( { - {\theta _k}\left| {x_i^k - x_j^k} \right|} \right) } \\ \hline {EXPG} & { \exp \left( { - {\theta _k}{{\left| {x_i^k - x_j^k} \right|}^{{\theta _{n + 1}}}}} \right),0 < {\theta _{n + 1}} \le 2 } \\ \hline {GAUSS} & { \exp \left( { - {\theta _k}{{\left| {x_i^k - x_j^k} \right|}^2}} \right) } \\ \hline {LIN} & {\max \left\{ {0,1 - {\theta _k}\left| {x_i^k - x_j^k} \right|} \right\} } \\ \hline {SPHERICAL} & { 1 - 1.5{\xi _k} + 0.5\xi _k^3,{\xi _k} = \min \left\{ {1,{\theta _k}\left| {x_i^k - x_j^k} \right|} \right\} } \\ \hline {CUBIC} & {1 - 3{\xi _k} + 2\xi _k^3,{\xi _k} = \min \left\{ {1,{\theta _k}\left| {x_i^k - x_j^k} \right|} \right\}} \\ \hline {SPLINE} & {\varsigma \left( {\xi _k} \right) , {\xi _k} = {\theta _k}\left| {x_i^k - x_j^k} \right|} \\ \hline \end{array} $$ $$\varsigma \left( {{\xi _k}} \right) = \left\{ \begin{array}{l}1 - 15\xi _k^2 + 30\xi _k^3,0 \le {\xi _k} \le 0.2\\1.25{\left( {1 - {\xi _k}} \right)^3},0.2 < {\xi _k} < 1\\0,{\xi _k} \ge 1\end{array} \right.$$$\theta$的最大似然估计值
我已经懒得敲公式了,基本思路就是刘俊老师的博士论文7所写的,这里贴出我论文中写的:

式(3.20)就是本文中式(4)!
到这里,Kriging模型的推导大致就结束啦!从上面推导可以看出,Kriging模型就是根据无偏估计和均方差最小两个条件得到的,但此时还有参数未确定,在给定样本情况下推参数,采用最大似然估计。
其实上述推导大多内容都来自前面dace工具箱所带的说明书,所以说学好英语很重要哈哈!
推导完Kriging模型,感觉影响其精度最重要的参数无非就是相关函数R的选取以及后面参数$\theta$的估计值,这也体现在dace工具箱的运用上!也有老师做过相关研究,利用一些算法寻找最优$\theta$值。
参考资料
1. https://www.bilibili.com/video/BV1Xr4y147nu/?spm_id_from=333.1007.top_right_bar_window_custom_collection.content.click&vd_source=41769b252ab81d02e47e5775242eda15 ↩
2. https://www.omicron.dk/dace.html ↩
3. https://xg1990.com/blog/archives/222 ↩
4. 韩忠华. Kriging模型及代理优化算法研究进展[J]. 航空学报, 2016, 37(11): 3197-3225. ↩
5. https://www.omicron.dk/dace/dace.pdf ↩
6. 查从燚,孙志礼,刘勤等.基于Kriging模型的液压管道防油击可靠性分析[J/OL].兵工学报:1-7[2024-03-23]. ↩
7. 刘俊. 基于代理模型的高效气动优化设计方法及应用[D]. 西北工业大学, 2017. ↩
8. https://www.bilibili.com/video/BV1QM4y167oZ/?spm_id_from=333.337.search-card.all.click&vd_source=41769b252ab81d02e47e5775242eda15 ↩