BP神经网络
BP神经网络
Charm_Hu说明
本文是基于B站UP主神罗Noctis的文档修改的,并参考了一些资料1,特此说明!
$BP$神经网络
1.激活函数
激活函数(Activation Function)是在人工神经网络的神经元上运行的函数,负责将神经元的输入映射到输出端。激活函数对于人工神经网络模型去学习、理解复杂的非线性函数,具有十分重要的作用。
如果不使用激活函数,每一层输出都是上一层输入的线性运算,无论神经网络有多少层,最终的输出只是输入的线性组合,相当于感知机。如果使用了激活函数,将非线性因素引入到网络中,使得神经网络可以任意逼近任何非线性函数,能够应用到更多的非线性模型。
常用的激活函数
$sigmoid$ 函数
$Sigmoid$函数是一个在生物学中常见的S型函数,也称为S型生长曲线。在信息科学中,由于其单增以及反函数单增等性质,Sigmoid函数常被用作神经网络的阈值函数,将变量映射到0,1之间,公式如下:

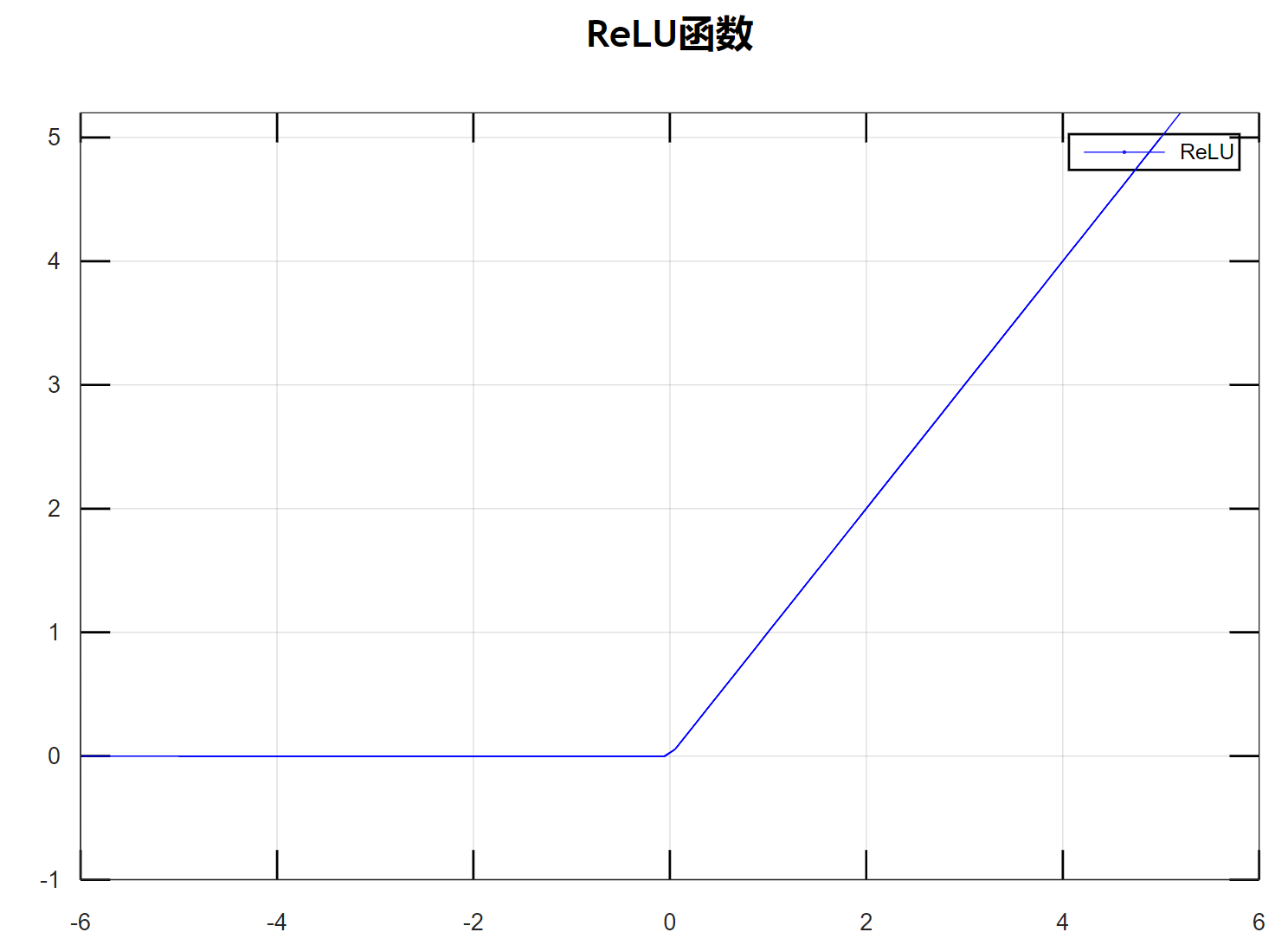
$ReLU$函数
$Relu$激活函数(The Rectified Linear Unit),用于隐藏层的神经元输出。公式如下:
$Tanh$ 函数
$Tanh$ 是双曲函数中的一个,$Tanh()$ 为双曲正切。在数学中,双曲正切“$Tanh$”是由基本双曲函数双曲正弦和双曲余弦推导而来。公式如下:
$softmax$ 函数
$softmax$ 函数用于输出层。假设输出层共有 $n$ 个神经元,计算第 $k$ 个神经元的输出 $y_k$。$softmax$ 函数的分子是输入信号 $a_k$ 的指数函数,分母是所有输入信号的指数函数的和。$softmax$ 函数公式如下:
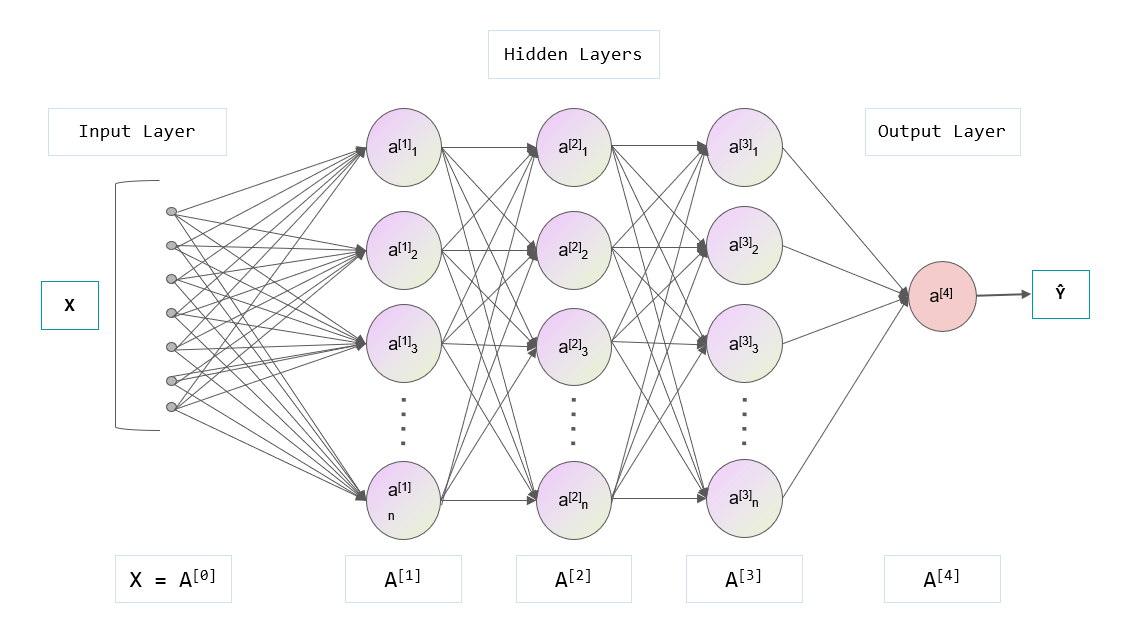
2.神经网络结构
第0层是输入层(2个神经元),第1层是隐含层(3个神经元),第2层是隐含层(2个神经元),第3层是输出层。
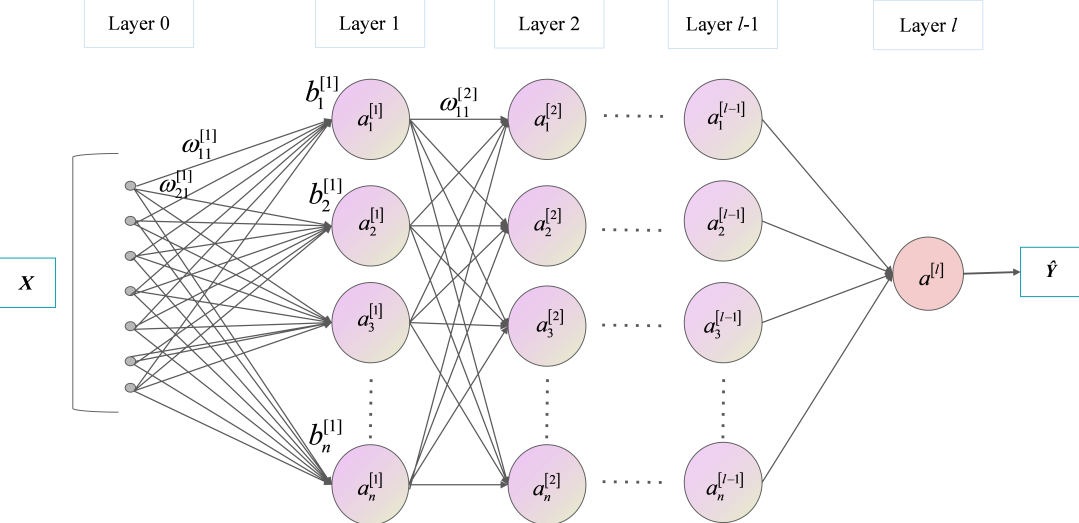
符号约定
$w_{j k}^{[l]}$表示从网络第$(l-1)^{t h}$ 层第$k^{t h}$ 个神经元指向第 $l^{t h}$ 层第 $j^{t h}$ 个神经元的连接权重,同时也是第 $l$ 层权重矩阵第 $j$ 行第 $k$ 列的元素。例如,上图中 $w_{21}^{[1]}$ ,第0层第1个神经元指向第1层第2个神经元的权重(褐色),也就是第 1 层权重矩阵第 2 行第 1 列的元素。同理,使用 $b_{j}^{[l]}$ 表示第 $l^{t h}$ 层第 $j^{t h}$ 个神经元的偏置 ,同时也是第 $l$ 层偏置向量的第 $j$ 个元素。使用 $z_{j}^{[l]}$ 表示第 $l^{t h}$ 层第 $j^{t h}$ 个神经元的线性结果,使用 $a_{j}^{[l]}$ 来表示第 $l^{t h}$ 层第 $j^{t h}$ 个神经元的激活函数输出。其中,激活函数使用符号σ表示,第 $l^{t h}$ 层中第 $j^{t h}$ 个神经元的激活为:
$w^{[l]}$ 表示第 $l$ 层的权重矩阵,$b^{[l]}$ 表示第 $l$ 层的偏置向量,$a^{[l]}$ 表示第 $l$ 层的神经元向量,结合上图讲述:
进行线性矩阵运算。
那么,前向传播过程可以表示为:
上述讲述的前向传播过程,输入层只有1个列向量,也就是只有一个输入样本。对于多个样本,输入不再是1个列向量,而是m个列向量,每1列表示一个输入样本。m个$a^{[l-1]}$列向量组成一个m列的矩阵$A^{[l-1]}$。
多样本输入的前向传播过程可以表示为:
与单样本输入相比,多样本$w^{[l]}$和$b^{[l]}$的定义是完全一样的,不同的只是$Z^{[l]}$和$A^{[l]}$从1列变成m列,每1列表示一个样本的计算结果。
3.损失函数
在有监督的机器学习算法中,我们希望在学习过程中最小化每个训练样例的误差。通过梯度下降等优化策略完成的,而这个误差来自损失函数。
损失函数用于单个训练样本,而成本函数是多个训练样本的平均损失。优化策略旨在最小化成本函数。下面例举几个常用的损失函数。
回归问题
- 绝对值损失函数($L_{1}$损失函数):
$L(\hat{y},y)=|y-\hat{y}|$
$y$ 表示真实值或期望值,$\hat{y}$ 表示预测值
- 平方损失函数($L_{2}$损失函数):
$L(\hat{y},y)=(y-\hat{y})^{2}$
$y$ 表示真实值或期望值,$\hat{y}$ 表示预测值
上述表达式是针对输出为1维的,如果输出多维,那么y就是一个列向量。
分类问题
- 交叉熵损失:
$L(\hat{y}, y)=-y \log (\hat{y})-(1-y) \log (1-\hat{y})$
$y$ 表示真实值或期望值,$\hat{y}$ 表示预测值
4.反向传播
反向传播的基本思想:通过计算输出层与期望值之间的误差来调整网络参数,使得误差变小(最小化损失函数或成本函数)。反向传播基于四个基础等式,非常简洁优美,但想要理解透彻还是挺烧脑的。
求解梯度矩阵
假设函数 $f:R^{n \times 1} \rightarrow R$ 将输入的列向量(shape: $n \times 1$ )映射为一个实数。那么,函数 $f$ 的梯度定义为:
$\nabla_{x} f(x)=\left[\begin{array}{c}\frac{\partial f(x)}{\partial x_{1}} \\ \frac{\partial f(x)}{\partial x_{2}} \\ \vdots \\ \frac{\partial f(x)}{\partial x_{n}}\end{array}\right]$
同理,假设函数 $f: R^{m \times n} \rightarrow R$ 将输入的矩阵(shape: $m \times n$ )映射为一个实数。函数 $f$ 的梯度定义为:
$\nabla_{A} f(A)=\left[\begin{array}{cccc}\frac{\partial f(A)}{\partial A_{11}} & \frac{\partial f(A)}{\partial A_{12}} & \dots & \frac{\partial f(A)}{\partial A_{13}} \\ \frac{\partial f(A)}{\partial A_{21}} & \frac{\partial f(A)}{\partial A_{22}} & \dots & \frac{\partial f(A)}{\partial A_{2 n}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial f(A)}{\partial A_{m 1}} & \frac{\partial f(A)}{\partial A_{m 2}} & \dots & \frac{\partial f(A)}{\partial A_{m n}}\end{array}\right]$
可以简化为:
$\left(\nabla_{A} f(A)\right)_{i j}=\frac{\partial f(A)}{\partial A_{i j}}$
注意:梯度求解的前提是函数 $f$ 返回的必须是一个实数,如果函数返回的是一个矩阵或者向量,是没有办法求解梯度的。例如,函数$f(A) =\sum_{i=0}^{m} \sum_{j=0}^{n} A_{i j}^{2}$,函数返回一个实数,可以求解梯度矩阵。如果 $f(x)=A x\left(A \in R^{m \times n}, x \in R^{n \times 1}\right),$ 函数返回一个m行的列向量,就不能对 $f$ 求解梯度矩阵。
矩阵相乘
矩阵 $A=\left[\begin{array}{cc}1 & 2 \\ 3 & 4\end{array}\right]$,矩阵 $B=\left[\begin{array}{cc}-1 & -2 \\ -3 & -4\end{array}\right]$
$A B=\left[\begin{array}{ll}1 \times-1+2 \times-3 & 1 \times-2+2 \times-4 \\ 3 \times-1+4 \times-3 & 3 \times-2+4 \times-4\end{array}\right]=\left[\begin{array}{cc}-7 & -10 \\ -15 & -22\end{array}\right]$
矩阵对应元素相乘
使用符号$\odot$表示:
$A \odot B=\left[\begin{array}{cc}1 \times-1 & 2 \times-2 \\ 3 \times-3 & 4 \times-4\end{array}\right]=\left[\begin{array}{cc}-1 & -4 \\ -9 & -16\end{array}\right]$
梯度下降法
从几何意义,梯度矩阵代表了函数增加最快的方向,沿着梯度相反的方向可以更快找到最小值。
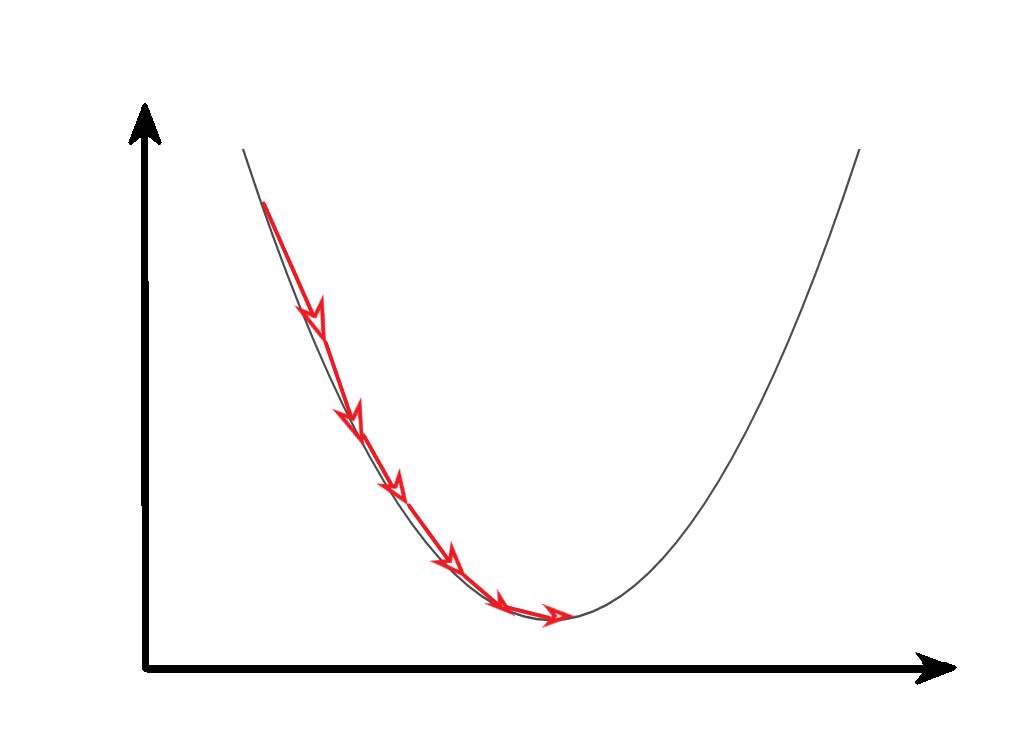
反向传播的过程就是利用梯度下降法原理,逐步找到成本函数的最小值,得到最终的模型参数。
反向传播公式推导(四个基础等式)
要想最小化成本函数,需要求解神经网络中的权重 $w$ 和偏置 $b$ 的梯度,再用梯度下降法优化参数。求解梯度也就是计算偏导数 $\frac{\partial L\left(a^{[L]}, y\right)}{\partial w_{j k}^{[l]}}$ 和 $\frac{\partial L\left(a^{[L]}, y\right)}{\partial b_{j}^{[l]}}$ 。为了计算这些偏导数,引入一个中间变量 $\delta_{j}^{[l]}$,它表示网络中第 $l^{t h}$ 层第 $j^{t h}$ 个神经元的误差。反向传播能够计算出误差$\delta_{j}^{[l]},$ 再根据链式法则求出 $\frac{\partial L\left(a^{[L]}, y\right)}{\partial w_{j k}^{[l]}}$ 和 $\frac{\partial L\left(a^{[L]}, y\right)}{\partial b_{j}^{[l]}}$ 。
定义网络中第 $l$ 层第 $j$ 个神经元的误差为 $\delta_{j}^{[l]}$ :
其中 $L(a^{[L]},y)$ 表示损失函数,$y$ 表示真实值,$a^{[L]}$ 表示输出层的预测值。
每一层的误差向量可以表示为:
等式一 输出层误差
L表示输出层层数。以下用 $\partial L$ 表示 $\partial L\left(a^{[L]}, y\right)$
写成矩阵形式是:
表示成公式:
推导
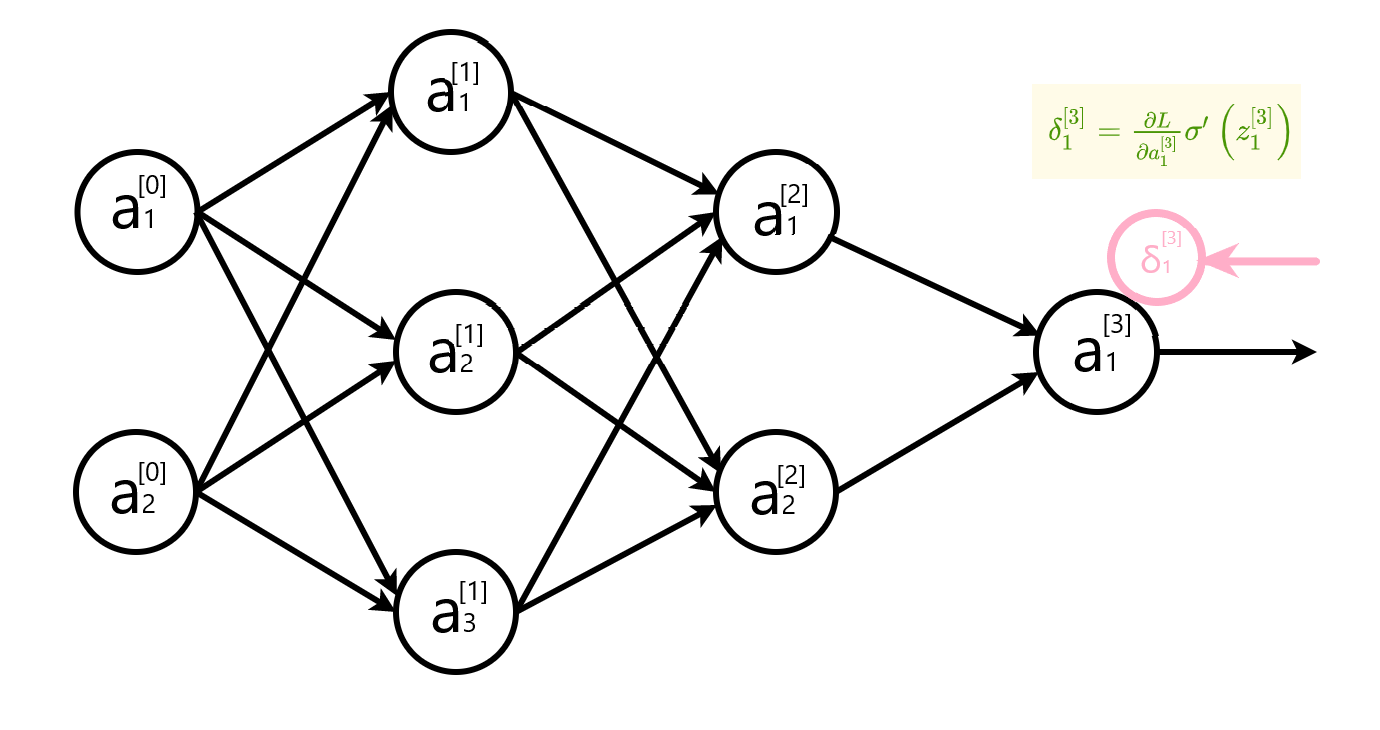
计算输出层的误差 $\delta_{j}^{[L]}=\frac{\partial L}{\partial z_{j}^{[L]}}$ ,根据链式法则
看起来上面式子很复杂,但是由于第k个神经元的输出激活值$a_k^l$只依赖于$z_k^l$。当$k≠j$时$\partial a^L_k / \partial z^L_j$消失了。于是上式简化为:
$\sigma$ 表示激活函数,由$a_{j}^{[L]}=\sigma\left(z_{j}^{[L]}\right)$,计算出 $\frac{\partial a_{j}^{[L]}}{\partial z_{j}^{[L]}}=\sigma^{\prime}\left(z_{j}^{[L]}\right)$ ,代入最后得到
等式二 隐藏层误差
写成矩阵形式:
推导
对 $z_{j}^{[l]}$ 求偏导,由于两层神经网络时间任意一对神经元只有一条连接,即$z_k^{l+1}$和$z_j^l$之间只通过$w_{kj}^{l+1}$连接,故
根据链式法则
其中用到:
等式三 参数变化率
推导
L 对 $b_{j}^{[l]}$ 求偏导,根据链式法则得到
L 对 $w_{j k}^{[l]}$ 求偏导,根据链式法则得到
等式四 参数更新
根据梯度下降法原理,朝着梯度的反方向更新参数
写成矩阵形式:
这里的 $\alpha$ 指的是学习率。学习率决定了反向传播过程中梯度下降的步长。
反向传播图解
计算输出层误差
计算隐藏层误差

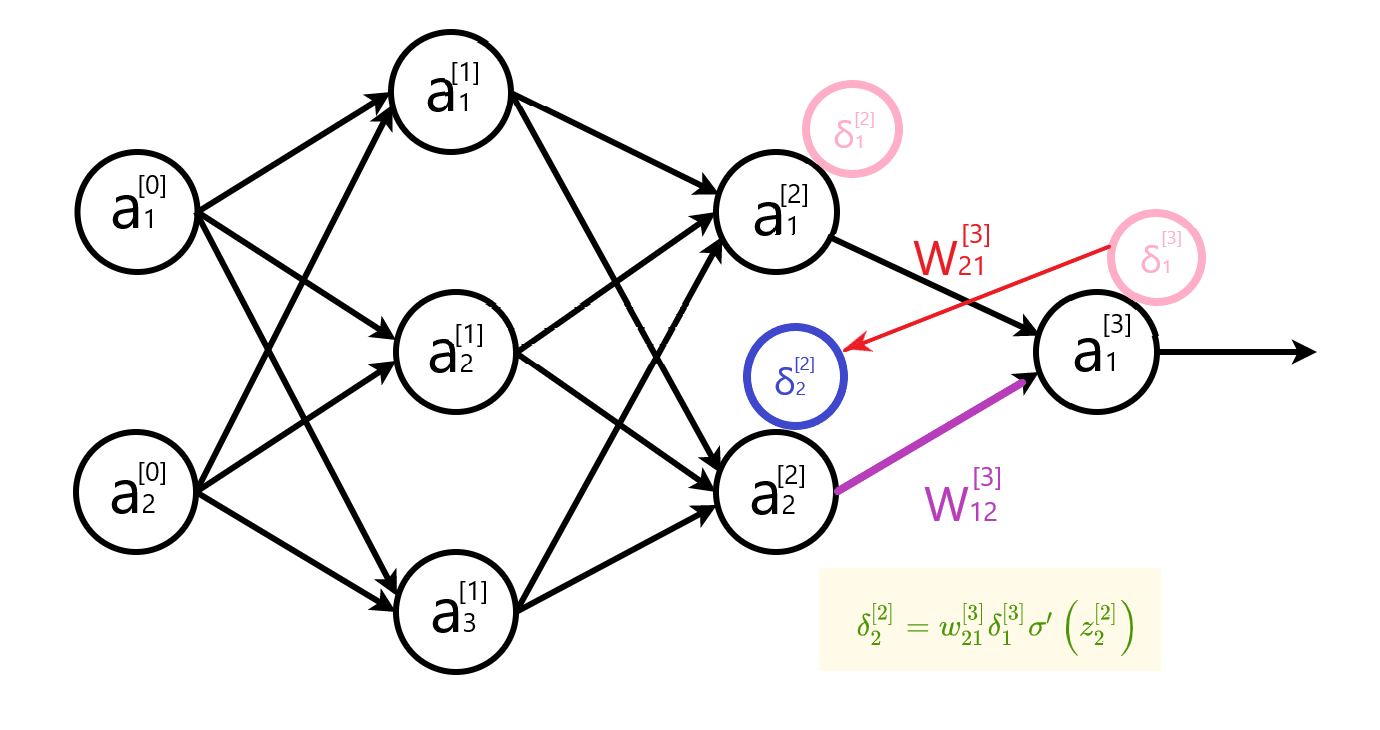
隐藏层误差公式写成矩阵形式 $\delta^{[l]}=\left[w^{[l+1]^{T}} \delta^{[l+1]}\right] \odot \sigma^{\prime}\left(z^{[l]}\right)$ 时, 权重矩阵需要转置。下面两幅图,直观地解释了转置的原因。
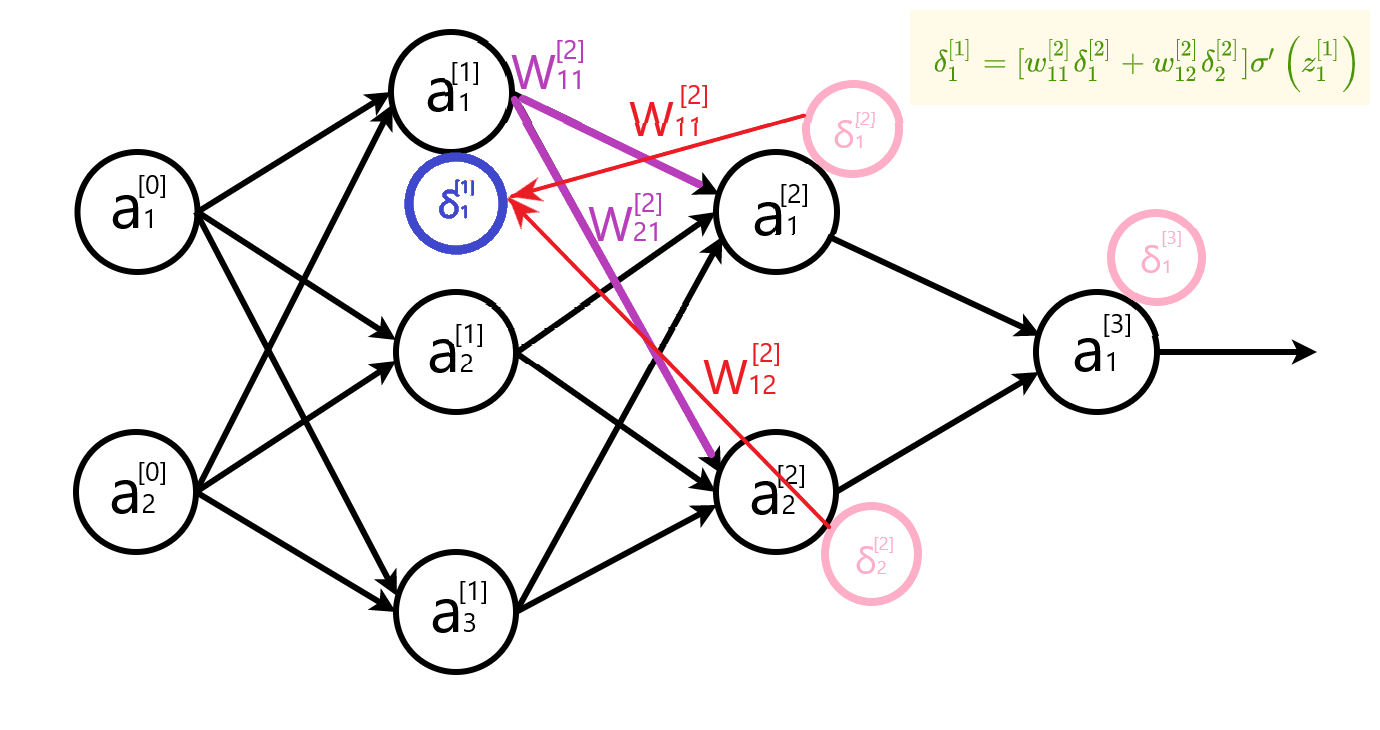
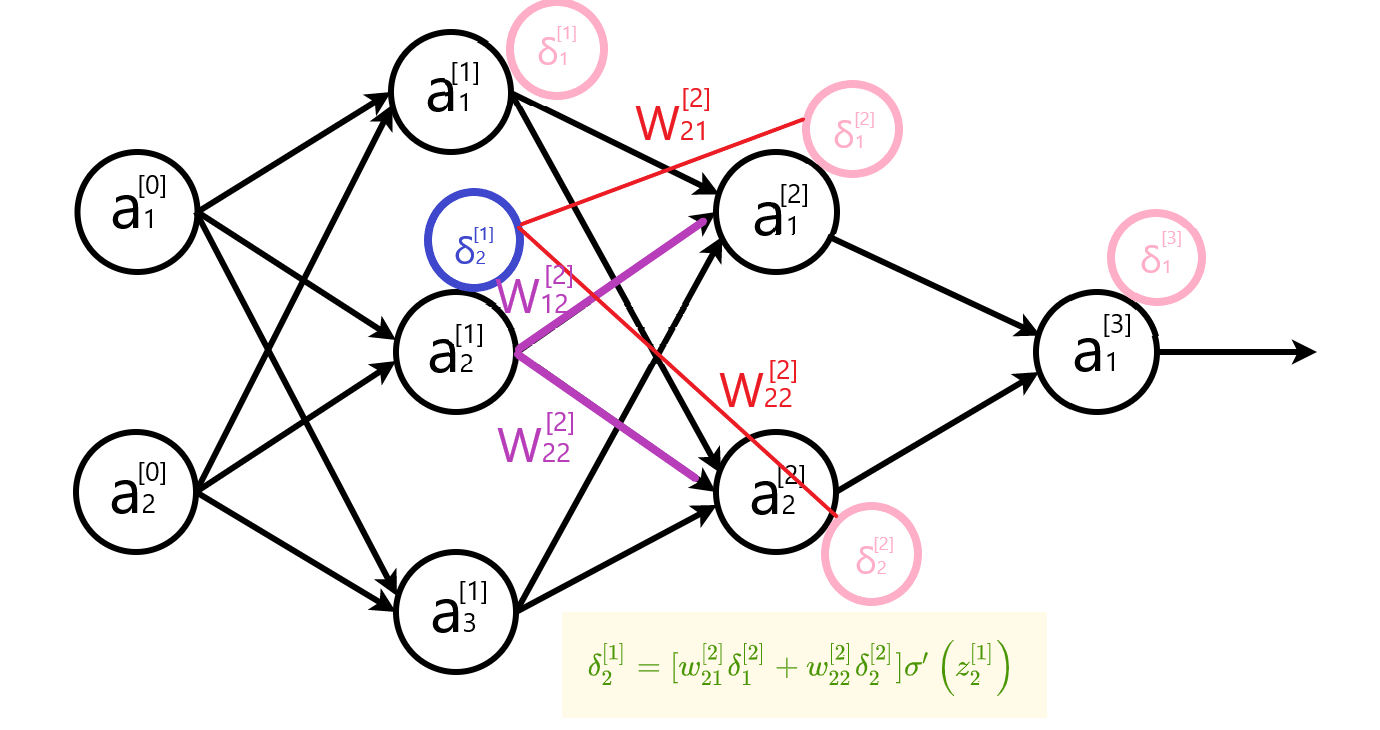

计算参数变化率
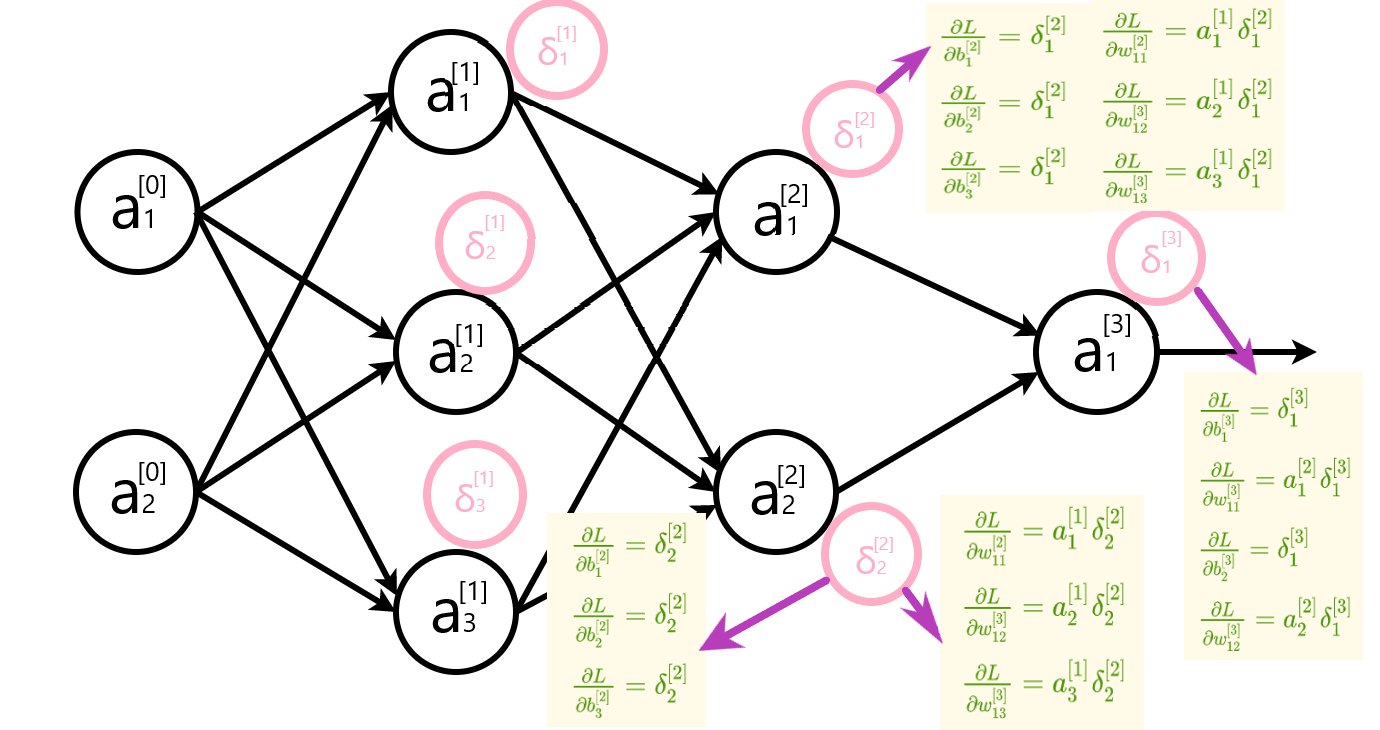
最后更新每层的参数。
反向传播公式总结
单样本输入公式表
| 说明 | 公式 |
|---|---|
| 输出层误差 | $\delta^{[L]}=\nabla_{a} L \odot \sigma^{\prime}\left(z^{[L]}\right)$ |
| 隐含层误差 | $\delta^{[l]}=\left[w^{[l+1]^{T}} \delta^{[l+1]}\right] \odot \sigma^{\prime}\left(z^{[l]}\right)$ |
| 参数变化率 | $\begin{array}{c}\frac{\partial L}{\partial b^{[l]}}=\delta^{[l]} \\\frac{\partial L}{\partial w^{[l]}}=\delta^{[l]} (a^ {[l-1] } )^T\end{array}$ |
| 参数更新 |
多样本输入公式表
成本函数
多样本输入使用的成本函数与单样本不同。假设单样本的成本函数是交叉熵损失函数。
$L(a, y)=-[y \cdot \log (a)+(1-y) \cdot \log (1-a)]$
那么,对于m个样本输入,成本函数是每个样本的成本总和的平均值。
$C(A,y)=-\frac{1}{m} \sum_{i=0}^{m}\left(y^{(i)} \cdot \log \left(a^{(i)}\right)+\left(1-y^{(i)}\right) \cdot \log \left(1-a^{(i)}\right)\right)$
误差
单样本输入的每一层的误差是一个列向量
而多样本输入的每一层的误差不再是一个列向量,变成一个m列的矩阵,每一列对应一个样本的向量。那么多样本的误差定义为:
$dZ^{[l]}$的维度是 $n×m$ ,$j$ 表示第 $l$ 层神经元的个数,$m$ 表示样本数量。
参数变换率
因为$dZ^{[l]}$的维度是 $n×m$ ,更新 $b^{[l]}$ 的时候需要对每行求和,再乘以$\frac{1}{m}$。
$dZ^{[l]}$的维度是 $n×m$ ,$(A^{[l-1]} )^T $ 的维度是 $m×s$,($s$是第$l-1$层神经元个数),矩阵相乘得到的维度是 $n×s$ ,与$w^{[l]}$ 本身的维度相同。因此更新 $w^{[l]}$ 时只需乘以 $\frac{1}{m}$ 求平均值。
| 说明 | 公式 |
|---|---|
| 输出层误差 | $d Z^{[L]}=\nabla_{A^ { [L] } } C \odot \sigma^{\prime}\left(Z^{[L]}\right)$ |
| 隐含层误差 | $d Z^{[l]}=\left[w^{[l+1] T} d Z^{[l+1]}\right] \odot \sigma^{\prime}\left(Z^{[l)}\right]$ |
| 参数变化率 | $d b^{[l]}=\frac{\partial C}{\partial b^{[l]}}=\frac{1}{m} Sum O f E a c h R o w\left(d Z^{[l]}\right) \\dw^{[l]}=\frac{\partial C}{\partial w^{[l]}}=\frac{1}{m} d Z^{[l]} ( A^{ [l-1] } )^T$ |
| 参数更新 | $\begin{array}{l}b^{[l]} \leftarrow b^{[l]}-\alpha \frac{\partial C}{\partial b^{[l]}} \\w^{[l]} \leftarrow w^{[l]}-\alpha \frac{\partial C}{\partial w^{[l]}}\end{array}$ |
参考资料
1. 反向传播算法-袁宵博客 ↩