弹塑性力学-张量分析
弹塑性力学-张量分析
Charm_Hu张量分析
张量基础
本想详细写一下张量分析基础的,奈何总是拖延,空不出时间来(敲公式太累,bushi),这里先放几个比较好理解的链接吧。
需要有一定的线性代数基础,否则这还是看不懂的。该痛苦的还是得痛苦,只不过希望你看完下面链接能有一种轻舟已过万重山的感觉。
总结来说,张量是一个不变量,在不同基下有不同坐标表达,于是衍生出利用坐标变换定义的张量的形式(1)和坐标分量加基矢量定义法(2)。
$$ \tag{1} {T_{{i_1}{i_2}...{i_n}}} = {\beta _{{i_1}{j_1}}}{\beta _{{i_2}{j_2}}}...{\beta _{{i_n}{j_n}}}{T_{{j_1}{j_2}...{j_n}}}$$
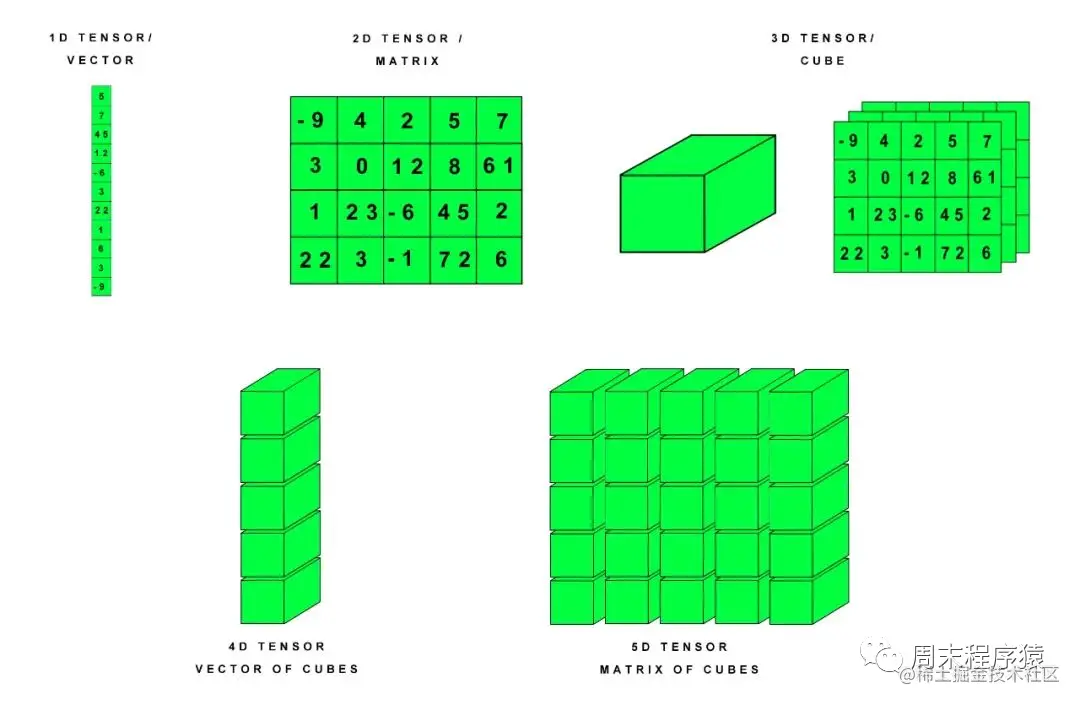
$$ \tag{2} \mathbf{T} = {T_{{i_1}{i_2}...{i_n}}}{e_{{i_1}}} \otimes {e_{{i_2}}} \otimes ... \otimes {e_{{i_n}}} $$$i_1$取1、2、3,其余指标同理; $ {T_{ {i_1} {i_2}…{i_n} } } $是张量$\mathbf{T}$的一个分量,一共$3^n$个这样的分量的有序集合构成一个n阶张量$\mathbf{T}$。
最简单的,例如一阶张量,即向量,其定义方式为$ \mathbf{T} = {T_i}{e_i}$,这样对比理解就好了。注意,此处$e_i$都是一阶张量(向量).
当然,很多人直接站在高维角度说,张量本质是线性映射。这句话是站在张量应用角度来说的,举几个简单例子,也可仔细阅读链接3、4。
- 质量:零阶张量,可以将加速度向量映射成力向量。(此处为线性变换,之所以称线性映射是为了更加普遍的情况)
- 应力张量:二阶张量,可以将截面位置映射为截面应力。(详见链接4:应力张量-线性映射)
虚功原理证明
学了张量分析,总得用一用它吧,看它在证明虚功原理上有多方便!
csdn上一篇文章也写得不错,可以参考一下:力学有限元的基石:虚功原理的推导
评论
匿名评论隐私政策