随机地震动生成
随机地震动生成
慕风随机地震动生成
基本理论
Clough-Penzien 谱
Clough-Penzien 谱是由 Clough 和 Penzien 提出的经典地震动功率谱模型,广泛应用于模拟地震动输入的频率特性,特别适用于结构动力分析中的输入地震动建模。它考虑了地震波从基岩到地面传播过程中滤波效应,因此比简单白噪声模型更真实。Clough-Penzien 功率谱的数学表达式为
$$S(\omega ) = {{1 + 4{\zeta _g}^2{{\left( {{\omega \over {{\omega _g}}}} \right)}^2}} \over {{{\left[ {1 - {{\left( {{\omega \over {{\omega _g}}}} \right)}^2}} \right]}^2} + 4{\zeta _g}^2{{\left( {{\omega \over {{\omega _g}}}} \right)}^2}}} \cdot {{{{\left( {{\omega \over {{\omega _s}}}} \right)}^4}} \over {{{\left[ {1 - {{\left( {{\omega \over {{\omega _s}}}} \right)}^2}} \right]}^2} + 4\zeta _s^2{{\left( {{\omega \over {{\omega _s}}}} \right)}^2}}}{S_0}$$其中,$S_0$为谱强度因子,一般需要根据PGA来调整,使得模拟得到的加速度时程具有与目标PGA相匹配的峰值,此处取0.005;$\omega _g$和$\zeta _g$分别表示地基土的卓越频率和阻尼比,$\omega _s$和$\zeta _s$分别是高通滤波器的两个参数,它们通过衰减低频分量的功率谱密度,确保地震时程的速度和位移积分具有物理意义,避免出现Kanai-Tajimi谱中位移发散的非物理结果。对于和的取值,陈国兴等学者的研究1指出,取${\xi _s} = {\xi _g}$,${\omega _s} = (0.1\sim0.2) {\omega _g}$。
针对四类场地,若要确定其卓越频率,还要考虑设计地震分组,以上海市为例,其设计地震分组为第一组,则四类场地类别的卓越频率如表1所示。取${\omega _s} = 0.1{\omega _g}$,地基土阻尼比${\xi _g}$的值参考文献2。
表1 四类场地对应的C-P模型参数
| 场地类别 | $\omega_g$ (rad/s) | $\xi_g$ | $\omega_s$ (rad/s) | $\xi_s$ |
|---|---|---|---|---|
| I₀ | 31.416 | 0.64 | 3.1416 | 0.64 |
| II | 17.952 | 0.72 | 1.7952 | 0.72 |
| III | 13.963 | 0.80 | 1.3963 | 0.80 |
| IV | 9.666 | 0.90 | 0.9666 | 0.90 |
注:由于Ⅰ类场地包含两个亚类I0和I1,此处仅以I0为例。
谱表达与随机谐和函数方法
谱表达方法是一种经典的平稳随机过程模拟方法,其核心思想是利用已知功率谱密度函数 ,通过一组频率分量的叠加,在时域中合成出一个与目标谱相符的地震动时程。谱表达方式通常采用如下形式:
$$a(t) = \sum\limits_{i = 1}^N {\sqrt {2S({\omega _i})\Delta \omega } } \cos ({\omega _i}t + {\phi _i})$$
其中 $\varphi_i$ 是在 $[0,2\pi]$ 之间均匀分布的独立随机变量,$\omega_i = \omega_{\min} + \left(i - \frac{1} {2} \right) \Delta\omega$。本文取$\omega_l = 0.1 \text{ rad/s},\quad \omega_u = 100 \text{ rad/s},\quad N = 1000,\quad \Delta\omega = \frac{ \omega_u - \omega_l} {N}$。
随机谐和函数法在谱表达法基础上考虑频率$\omega_{i}$也为独立随机变量,在$\left[ { {\omega _l},{\omega _u} } \right]$上满足均匀分布。
然而上述两种方法得到的是平稳随机过程,需要乘以时间包络函数,得到的地震动时程才能够大体反映地震动的时域非平稳特性。时间包络函数3选取如下:
$$f(t) =
\begin{cases}
\left(\frac{t}{t_1}\right)^2 & 0 \le t \le t_1 \\
1 & t_1 \le t \le t_2 \\
e^{-c(t-t_2)} & t \ge t_2
\end{cases}$$
其中,$t_1$ 取 $2\text{ s}$,$t_2$ 取 $15\text{ s}$,$c$ 取 $0.45$。地震动持时 $t_d = 20\text{ s}$。
为了验证所生成的地震动时程是否符合Clough-Penzien模型的谱特征,本文将每条模拟加速度时程转换为功率谱密度(PSD),并与目标谱进行对比。本文采用Welch方法(MATLAB中的pwelch()函数)进行PSD估计。Welch方法基本原理是把时程$a(t)$拆分成多个重叠的小段,每段计算其快速傅里叶变换(FFT),然后平方取模,得到每段的功率谱;最后对多个小段进行平均,得到平滑的PSD估计值。
生成地震动加速度时程及其PSD
本文基于Clough-Penzien谱利用MATLAB,针对四类场地,生成10条随机地震动,相应代码如下。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121clc
clear all
%% 通用参数
N = 1000; % 频率离散点数
dt = 0.001; % 时间步长 (s)
T = 20; % 总时长 (s)
t = 0:dt:T; % 时间向量
omega_min = 0.1; % 最小角频率 (rad/s)
omega_max = 100; % 最大角频率 (rad/s)
S0 = 0.005; % 归一化常数
numReals = 10; % 每种方法生成的随机地震条数
fs = 1/dt; % 采样频率
% 四类场地 Clough-Penzien 谱参数
siteClasses = {'I0','II','III','IV'};
CP = struct();
CP.I0 = struct('omega_g',31.416,'zeta_g',0.64,'omega_s',3.1416,'zeta_s',0.64);
CP.II = struct('omega_g',17.952,'zeta_g',0.72,'omega_s',1.7952,'zeta_s',0.72);
CP.III = struct('omega_g',13.963,'zeta_g',0.80,'omega_s',1.3963,'zeta_s',0.80);
CP.IV = struct('omega_g',9.666,'zeta_g',0.90,'omega_s',0.9666,'zeta_s',0.90);
% 创建保存目录
baseDir = fullfile(pwd,'地震动模拟结果');
folders = {fullfile(baseDir,'地震动时程'), fullfile(baseDir,'PSD')};
for k=1:numel(folders)
if ~exist(folders{k},'dir')
mkdir(folders{k});
end
end
% 目标谱函数句柄
SY_fun = @(w,cp) (1+4*cp.zeta_g^2*(w/cp.omega_g).^2)./((1-(w/cp.omega_g).^2).^2+4*cp.zeta_g^2*(w/cp.omega_g).^2) .* ...
((w/cp.omega_s).^4./((1-(w/cp.omega_s).^2).^2+4*cp.zeta_s^2*(w/cp.omega_s).^2))*S0;
% 主循环:场地类别
for s = 1:length(siteClasses)
site = siteClasses{s};
cp = CP.(site);
% 频谱离散
delta_omega = (omega_max-omega_min)/N;
omega = omega_min + ( (1:N)-0.5 )*delta_omega;
sy_target = SY_fun(omega,cp);
% 存 PSD 目录
psdDir = fullfile(baseDir,'PSD',site);
if ~exist(psdDir,'dir'), mkdir(psdDir); end
% 存时程目录
accDir_spec = fullfile(baseDir,'地震动时程',site,'spectrum');
accDir_harm = fullfile(baseDir,'地震动时程',site,'harmonic');
if ~exist(accDir_spec,'dir'), mkdir(accDir_spec); end
if ~exist(accDir_harm,'dir'), mkdir(accDir_harm); end
% 生成多条
for method = {'spectrum','harmonic'}
m = method{1};
for k = 1:numReals
% 随机相位与频率
switch m
case 'spectrum'
phi = 2*pi*rand(1,N);
A = sqrt(2*SY_fun(omega,cp)*delta_omega);
acc = zeros(size(t));
for i = 1:N
acc = acc + A(i) * cos(omega(i) * t + phi(i));
end
case 'harmonic'
omega_r = sort(omega_min + (omega_max-omega_min)*rand(1,N));
delta_omega_r = diff([omega_r,omega_max]);
phi_r = 2*pi*rand(1,N);
A_r = sqrt(2*SY_fun(omega_r,cp).*delta_omega_r);
acc = zeros(size(t));
for i = 1:N
acc = acc + A(i) * cos(omega(i) * t + phi(i));
end
end
% 包络
t1=2; t2=15; c=0.45; fenv=zeros(size(t));
fenv(t<=t1)=(t(t<=t1)/t1).^2;
fenv(t>t1 & t<=t2)=1;
fenv(t>t2)=exp(-c*(t(t>t2)-t2));
acc = acc.*fenv;
% 保存时程 MAT 和图像
fn = sprintf('%s_%s_%02d',site,m,k);
save(fullfile(baseDir,'地震动时程',site,m,[fn '.mat']),'t','acc');
figure('Visible','off');
plot(t,acc);
xlabel('t(s)');
ylabel('a(m/s^2)');
title(['Acceleration - ' site ' - ' m ' - #' num2str(k)]);
saveas(gcf,fullfile(baseDir,'地震动时程',site,m,[fn '.png']));
close;
end
end
% PSD 对比(以第一条为例)
% 读取第一条
d1 = load(fullfile(accDir_spec,[site '_spectrum_01.mat'])); acc1=d1.acc;
d2 = load(fullfile(accDir_harm ,[site '_harmonic_01.mat'])); acc2=d2.acc;
% 计算 PSD
[psd1,f] = pwelch(acc1,[],[],[],fs);
[psd2,~] = pwelch(acc2,[],[],[],fs);
w = 2*pi*f;
valid = w>=omega_min & w<=omega_max;
% 绘图保存
figure('Visible','off');
plot(w(valid),psd1(valid)/(2*pi),'m-','DisplayName','谱表达法');
hold on;
plot(w(valid),psd2(valid)/(2*pi),'b--','DisplayName','随机谐和函数法');
plot(omega,sy_target,'r-','DisplayName','C-P 目标谱');
legend;
xlabel('rad/s');
ylabel('PSD (m^2/s^3)');
title(['PSD Comparison - ' site]);
grid on;
xlim([omega_min omega_max]);
saveas(gcf,fullfile(psdDir,['PSD_' site '.png']));
close;
end
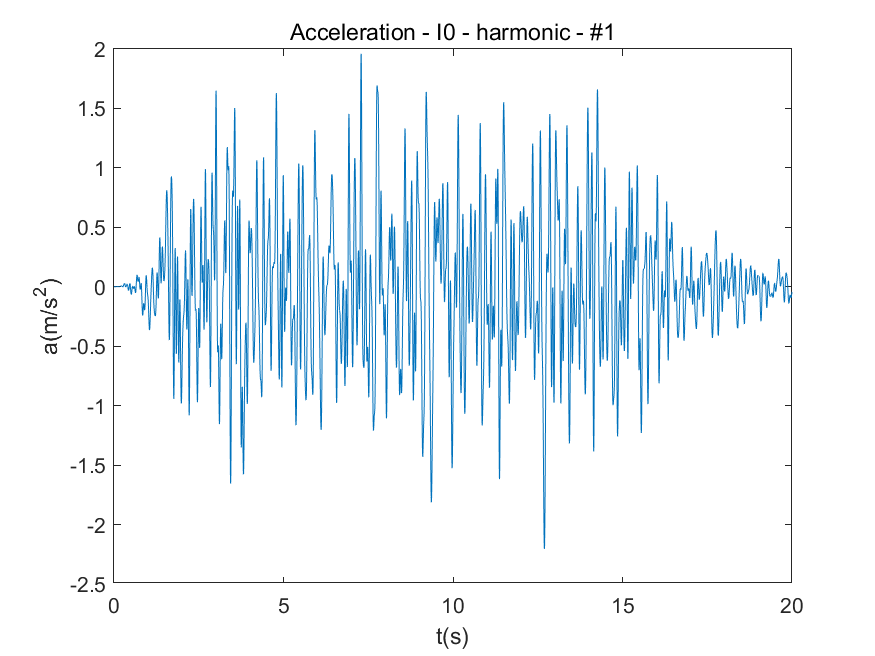
I0类场地下谱表达法生成的随机地震动:
I0类场地下谱表达法和随机谐和函数法获得的结果与目标谱对比:

参考文献
1. 陈国兴, 金永彬, 宰金珉. 高层建筑随机地震反应的简捷计算[J]. 南京建筑工程学院学报, 1999, (01): 31-39. ↩
2. 张治勇, 孙柏涛, 宋天舒. 新抗震规范地震动功率谱模型参数的研究[J]. 世界地震工程, 2000, (03): 33-38. ↩
3. AMIN M, ANG A H S. Nonstationary stochastic model of earthquake motion[J]. Journal of the Engineering Mechanics Division, ASCE, 1968, 94(EM2): 559-584. ↩